2^x 3^y=17 2^x 2-3^y 1=5 by elimination method 953104

First, you have to equate the coefficients of the y so equation 1 will be doubled 4x 2y = 0 x 2yView Homework Help Mod8 exercisedocx from MATH 140 at EmbryRiddle Aeronautical University Ch8 8) x y 3 z=9 3 x y 2 z =2 2 x 4 y 2=0 1 1 3 8 3 1 22 2 4 1 0 1 1 3 8 (3 ) 2^x3^y=17 2^x23^y1=5 And 2^x X 2^2 — 3^y X 3=5 A X 4 — B X 3=5 4A—3B=5 eq2 Solve eq1 and eq2 A=8 and B=9 Then 2^x=8 and 3^y=9 When using Gaussian elimination to solve a system of linear equations, explain how you can recognize that the system has no solution Give an example that illustrates your answer

What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora

2^x 3^y=17 2^x 2-3^y 1=5 by elimination method

2^x 3^y=17 2^x 2-3^y 1=5 by elimination method-Hence the solution to the system is (3, 2) This process describes the elimination (or addition) method A means of solving a system by adding equivalent equations in such a way as to eliminate a variable for solving linear systems Of course, the variable is not always so easily eliminated Typically, we have to find an equivalent system by applying the multiplication property of equalityAnswer to Solve by the elimination method 6x y = 26;

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 15 Question 1 Solve the following systems of linear equations by Gaussian elimination method (i) 2x – 2y 3z = 2, x 2y – z = 3, 3x – y 2z = 1 (ii) 2x 4y 6z = 22, 3x 8y 5z = 27, x y 2z = 2 SolutionAlgebra Solve by Addition/Elimination 2xy=3 3xy=17 2x y = −3 2 x y = 3 3x − y = −17 3 x y = 17 Add the two equations together to eliminate y y from the system 2 2X 3y = 17 By signing up, you'll get thousands of stepbystep solutions to your

View Solving Systems ALL Methodspdf from ECE MISC at University of South Florida IM 1 Name_ ID 1 Solving Systems using All Methods Date_ Period_ Solve each system by graphing 1) y = x 3 yTo solve this system of equation, substitution method can be applied To do so, solve for x in EQ2 `x y =2` `xyy=2y` `x=y2` Then, substitute this toElimination method x2y=2x5, xy=3 \square!

 X/22y/3=1 and xy/3=3 solve by elimination method 2 See answers KrishnaPolavarapu KrishnaPolavarapu Here's your answer Hope it was helpful EthicalElite EthicalElite x=1×2 x=2 Hence, solution is x=2 and y=3 Hope it helps you, Please mark me as brainlist New questions in MathClick here👆to get an answer to your question ️ Solve the system of equations 2x 3y = 17, 3x 2y = 6 by the method of cross multiplicationFree system of equations elimination calculator solve system of equations unsing elimination method stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy

Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions

Step By Step Math Wolfram Alpha Blog

About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or subtracting your equations together You can use this Elimination Calculator to practice solving systems> Solve by elimination method maths Solve by elimination method 3 x 3 y = 1 5 Solve the following pairs of linear (simultaneous) equation by the method of elimination by substitution 2 x 3 y = 8, 2 x = 2 3 y Medium View solution Solver for x and y 8 xElimination Method Steps Step 1 Firstly, multiply both the given equations by some suitable nonzero constants to make the coefficients of any one of the variables (either x or y) numerically equal Step 2 After that, add or subtract one equation from the other in such a way that one variable gets eliminatedNow, if you get an equation in one variable, go to Step 3

Solve The Equations 4 2 X 1 9 3 Y 1 17 And 3 2 X

Solve Each Of The Following Systems Of Equations Using Matrix Method X Y 3 2x 3y 4z 17 Y 2z 7

Question Need help solving system by elimination method x/2 y/3 = 7/6 2x/3 3y/4 = 5/4 Thank you Found 3 solutions by Alan3354, Fombitz, rothausercSolve the Following Pair of Linear (Simultaneous ) Equation Using Method of Elimination by Substitution 2( X 3 ) 3( Y 5 ) = 0 5( X 1 ) 4( Y 4 ) = 0Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Graph Graph Inequalities With Step By Step Math Problem Solver

2 X 3 Y 17 1 X 1 Y 7 Solv This With The Method Of Elimination Brainly In

 Add the equations to eliminate y and solve for x, and then substitute back to solve for y Starting with {(2x 5y = 17), (6x 5y = 9)} We wish to solve for one of the variables by eliminating the other with addition or subtraction Note that we have 5y in the first equation and 5y in the second This means we may eliminate the variable y without further manipulation (in a3x – 04y = 112 asked in Algebra by nchi ( 4k points) algebraA)0 ***** b)1 c)2 d)3 3solve How do I do this?(Math) Use the Substitution method to solve the system of equations y 2x = 5 3y x = 5 Solve one of the equations for x or y

If A 2 3 4 1 1 0 0 1 2 Find A 1 Hence Solve System Of

Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples

Solution Step 1 Select a variable which you want to eliminate from the equations Let us select y y 4x−3y = 32 xy = 1 4 x − 3 y = 32 x y = 1 Step 2 Take suitable constants and multiply them with the given equations so as to make the coefficients of the variable (which we want to eliminate)By elimination or by substitution I don't know which one is your preferred method so I will do both Both methods will yield the same answer Method 1 Elimination 2xy =0 x 2y = 5 Let us use x as the variable we want to work out; Solve this question with the elimination method X 2y = 4 Y = x 2 2 See answers texaschic101 texaschic101 Y = x 2 2 = x 2 add 2 to both sides Multiply both sides by 1/5 Multiply both sides by the reciprocal of 1/5 Divide 5 by both sides Divi de one side by 5 Adya and Ashley complete a work separately in and 25 days

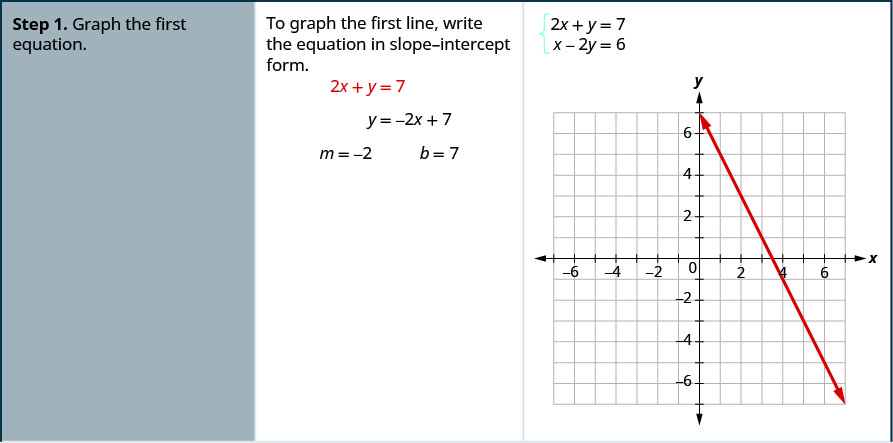
3a 4 Solve Systems Of Linear Equations With Two Variables Mathematics Libretexts

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

Solve this linear system using the elimination method 3x – y = 3 x y = 17 Good heavens, the y's are already lined up and signed up for us to eliminate them (3x x) (y y) = (3 17) 4x = x = 5 Plug x = 5 into the second original equation and solve for y 5 y = 17 y = 12 The solution seems to be (5, 12) Let's make a quick check for body doubles, evil clones, or demonic How many real number solutions are there to the equation 0=3x^2x4?2/3x3/5y=17 1/2x1/3y=1 Rewrite each equation by multiplying the LCD of each equation respectively 10x 9y = 255 3x 2y = 6 Use elimination method to solve this system

Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu

Step By Step Math Wolfram Alpha Blog

(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3 Transcript Example 7 Solve the following pair of equations by substitution method 7x – 15y = 2 x 2y = 3 7x – 15y = 2 x 2y = 3 From (1) 7x – 15y = 2 7x = 2 15y x = (𝟐 𝟏𝟓𝒚)/𝟕 Substituting the value of x in (2) x 2y = 3 (2 15𝑦)/7 2𝑦=3 Multiplying both sides by 7 7 × ((2 15𝑦)/7) 7×2𝑦=7×3 (2 15y) 14y = 21 15y 14y = 21 – 2 29y = 21 – 22x y = 2 5x 3y = 1 If a variable is not isolated in one of the equations in the system, solve an equation for a variable first Then you can use substitution

Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions

Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3

 Example 18 Solve the following pair of equations by reducing them to a pair of linear equations 5/(𝑥 −1) 1/(𝑦 −2) = 2 6/(𝑥 −1) – 3/(𝑦 −2) = 1 5/(𝑥 − 1) 1/(𝑦 − 2) = 2 6/(𝑥 − 1) – 3/(𝑦 − 2) = 1 So, our equations become 5u v = 2 6u – 3v = 1 Thus, our5x y = 9 (ii) 15x 01y = 62; Solve, using the method of substitution (i) 2x – 3y = 7;

How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora

3 Ways To Solve Systems Of Algebraic Equations Containing Two Variables

Elimination Using Addition Example #1 Solve the system shown below using the elimination method 3x – 2y = 1 –3x 4y = 7 Step 1 Think Are any terms that are the same or opposites?2x y = 3 6x 3y = 9 (equation 1) 7x 3y = 4 (equation 2) Adding equations (1) and (2) 13x = 13 x = 1 Substitute x = 1 into (1) 6(1) 3y = 9 6 3y = 9 y = 1 (x, y) = (1, 1)By elimination method 3xy7/112=10 2yx11/7=10 Ask questions, doubts, problems and we will help you

If 2x 3y 17 And 3x 5y 27 What Are X And Y Quora

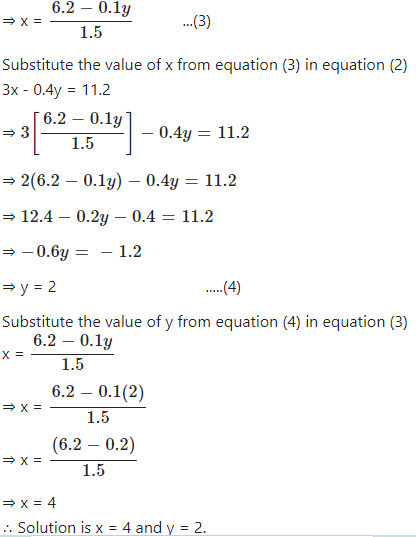
Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp

 Solve the system using the elimination method 2x3y=17 3xy=15 Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website By continuing to use this site you consent to the use of cookies on your device as described in our cookie policy unless you have disabled themSolve by Addition/Elimination x^2y^2=23 , xy=11 This system of equations cannot be solved using the addition method , but can be solved using substitution Can't be solved with addition methodThe elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

1

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Answer to Solve 2 x 3 y = 14 and 3 x 4 y = 4 by the method of elimination By signing up, you'll get thousands of stepbystep solutions toI Elimination method ii Substitution method we choose equation (2), then we would obtain, Solving simultaneous equations elimination Using the same equations from above, we will illustrate how to solve for x and y using the method of elimination (1) (2) In the method of elimination, we examine both

Solve By Reducing Them To A Pair Of Linear Equations 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Youtube

What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora

Math 1313 Section 32 Example 6 Solve the system of linear equations using the GaussJordan elimination method 3x 4y 4z 19 x 2y 3z 7 2x 4y 6z 38 Another way of solving the system of equations is by Elimination method That is a method where we tend to eliminate one variable to solve for the (25)^x 2y=08(128)^x 3y=17(1/5)^x''28 Questions Show answers Q 2 sodas and 3 hamburgers cost $850 6 sodas and 1 hamburger cost $950 Find how much a soda and hamburger cost Q Solve the system by elimination Q WRITE EQUATIONS The sum of Mr Micklow and Ms Craft's age is 55 The difference is 3

Solve This Q 2x 3y 172x 2 3y 1 5 Solve It By Elimination Or Substitution Method Maths Pair Of Linear Equations In Two Variables Meritnation Com

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

 Find an answer to your question Solve the system by the elimination method 2x 3y 10 = 0 4x 3y 2 = 0 When you eliminate y, what is the resulting equ TimeMunkee TimeMunkee Mathematics College answered Solve the system by the elimination method Let 2^x = t let 3 ^y = q qt = 17 qt =3 2q = when i add these both eqution q= 10 put q in eqution q t = 17 t= 7 now using log we can find x and y 2^x = 10 xlog 2 = 1 x= 1/log2 log 10 =1 as 7= 3^y log 7 /log 3 =y means y = log 7 base 3Download presentation Solving System of Linear Equations Elimination Method Warmup solve the linear system by Elimination y 2 x = 3 y x = 1 (2, 1)

Numerical Methods

Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf

Do the arithmetic x=9,y=2 Extract the matrix elements x and y \frac {1} {3}x5y=13,2x\frac {1} {2}y=19 In order to solve by elimination, coefficients of one of the variables must be the same in both equations so that the variable will cancel out when one equation is subtracted from the otherYou can put this solution on YOUR website!Solving System of Linear Equations Elimination Method Warmup Slides 10;

7 Y 3 2 X 2 14 4 Y 2 4 X 3 44 Solve Equation Using Elimination Method Brainly In

Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf

Solve the Following Systems of Equations `5/(X Y) 2/(X Y) = 1` `15/(X Y) 7/(X Y) = 10` Let `1/(x y) = u` and `1/(x y) = v`Then, the given system off equations becomesFind the value of y x – y = 0 x y= 2Find the value of y 3x 2y = 1 x 4y = 2 !

Solve The Following System Of Linear Equation Graphically 2x 3y 17 0 And 4x Y 13 0 Shade The Region Brainly In

Answers

 y = 2 x = 1 We can solve this one of two ways;Solving Linear Equations by Elimination Method Here we are going to see some example problems of solving linear equations in two variables using elimination method The various steps involved in the technique are given below Step 1 Multiply one or both of the equations by a suitable number (s) so that either the coefficients of firstIn this case, the 3x and –3x are opposites Step 2 Use the addition property of equality to combine the two equations into one 3x – 2y = 1

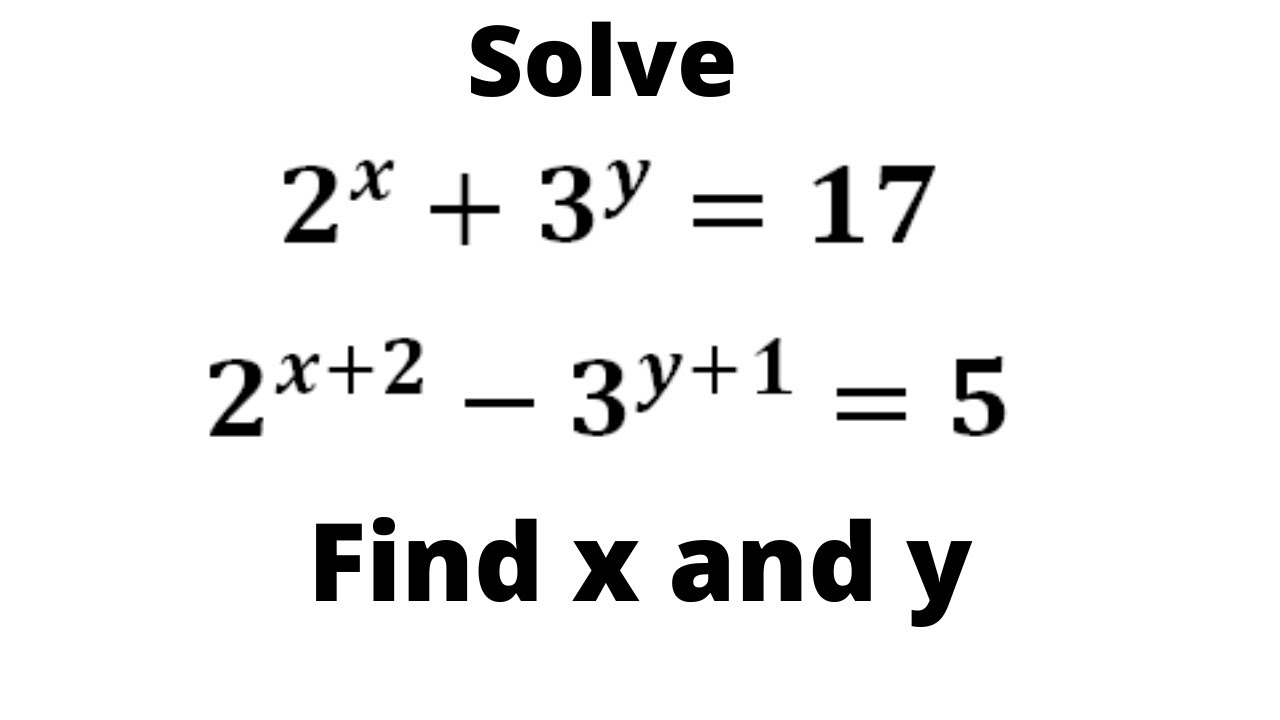
Solve 2 X 3 Y 17 2 X 2 3 Y 1 5 Find X And Y Youtube

Solve Solve Linear And Quadratic Equations With Step By Step Math Problem Solver

We will be using these same methods as we look at nonlinear systems of equations with two equations and two variables A system of nonlinear equations is a system where at least one of the equations is not linear For example each of the following systems is a system of nonlinear equations { x 2 y 2 = 9 x 2 − y = 9 { 9 x 2 y 2 = 9 y = 3

Solving A System Of Equations Using A Matrix Precalculus Socratic

5 3 Solve Systems Of Equations By Elimination Mathematics Libretexts

Solving Systems Of Linear Equations By Elimination Ppt Video Online Download

If 2x 3y 2 3 4 0 And 3x 2y 2 2 1 5 Find X And Y Youtube

Lo I Can Solve Simultaneous Equations Date

Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf

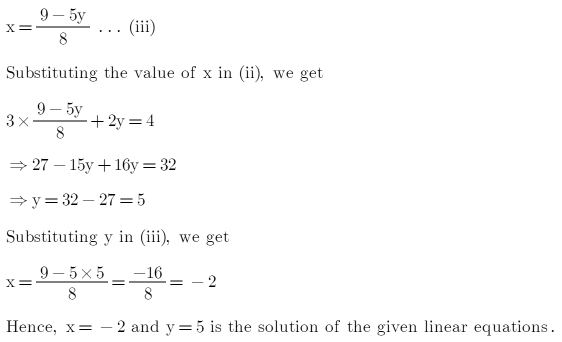
By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll

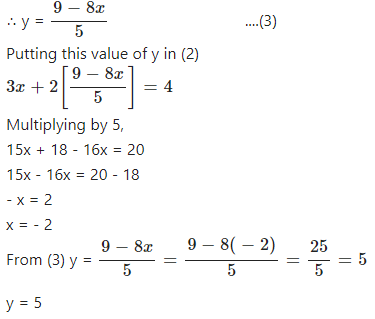
Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp

How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora

Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu

Systems Of Linear Equations

Show That The System Of Equations 2x 5y 17 5x 3y 14 Has A Unique Solution Find The Solution

Olve By Elimination Method 2power X 3 Power Y 17 2 Power X 2 3 Power Y 1 5 Maths Polynomials Meritnation Com

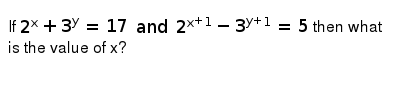
If 2 X 3 Y 17 And 2 X 1 3 Y 1 5 Then What Is The Val

Solve The Following Systems Of Equations 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2 Sarthaks Econnect Largest Online Education Community

Solving Linear Systems

Systems Of Equations With Elimination 3y 4x 11 Y 2x 13 Video Khan Academy

Solving A System Of Equations Using A Matrix Precalculus Socratic

Chapter 3 Pairs Of Linear Equations In Two Variables Rd Sharma Solutions For Class 10 Mathematics Cbse Topperlearning

Solving Linear Systems

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

2 X 3 3 Y 5 0 5 X 1 4 Y 4 0 Solve It By Substitution Method Brainly In

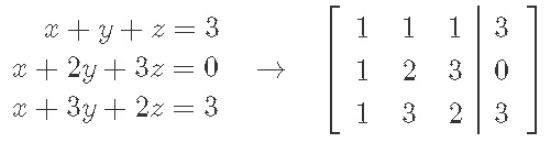
Systems Of Linear Equations Gaussian Elimination Studypug

Solving Linear Systems By Elimination

Solve Solve Linear And Quadratic Equations With Step By Step Math Problem Solver

Solve The Following Systems Of Equations 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2 Sarthaks Econnect Largest Online Education Community

3 Ways To Solve Systems Of Algebraic Equations Containing Two Variables

1

Search Q Solve 3x 2b2y 3d11 And 2x 2b3y 3d4 By Elimination Method Tbm Isch

Nms 2nd Lesson Ii

Chapter 3 Pairs Of Linear Equations In Two Variables Rd Sharma Solutions For Class 10 Mathematics Cbse Topperlearning

Solving Linear Systems

If 2 X 3 Y 17 And 2 X 1 3 Y 1 5 Then What Is The Val

Solve Graphically 5x Y 17 And 2x 2y 2plz Show In Graph And Algebraically Brainly In

Systems Of Linear Equations

X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube

Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline

Solving Linear Systems By Elimination

Solving Linear Systems By Substitution

If 3x 5y 9 And 5x 3y 7 Then Find The Value Of X Y Youtube

Solve The Equation To Find The Value Of X And Y Using Elimination Method Q 2x 3y 172x 2 3y 1 5 Maths Pair Of Linear Equations In Two Variables Meritnation Com

Solve The Following Systems Of Equations 15 U 2 V 17 1 U 1 V 36 5 Sarthaks Econnect Largest Online Education Community

3 Ways To Solve Systems Of Algebraic Equations Containing Two Variables

System Of Equations And Elimination Section 4 3 Overview Solving By The Elimination Method Problem Solving Ppt Download

Solving A System Of Equations Using A Matrix Precalculus Socratic

Solving A System Of Equations Using A Matrix Precalculus Socratic

Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples

Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 603 A1 c6 l2 solution key worked out Pdf

Solve The Following For X And Y By Using Method Of Elimination 2 X 3 Y 17 2 X 2 3 Y 1 5 Brainly In

Math Questions Math Answers

How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora

Step By Step Math Wolfram Alpha Blog

Q Tbn And9gcqxnk Lpfjle Erogd0wsraw D67yjyrnkghuofquiwt4u Rzfp Usqp Cau

Chapter 6 Simultaneous Linear Equations Including Problems Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning

Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples

Solutions To Problems In Chapter One Mathematics

Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf

Solving Systems Of Linear Equations By Elimination Ppt Video Online Download

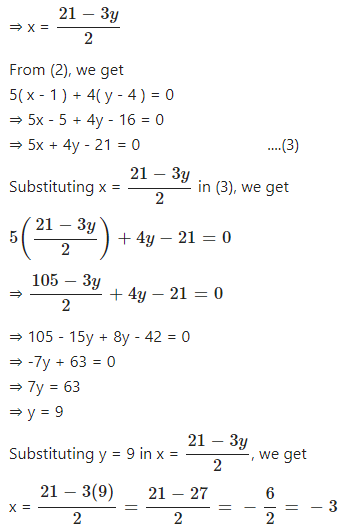
Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp

Step By Step Math Wolfram Alpha Blog

3 Ways To Solve Systems Of Algebraic Equations Containing Two Variables

If X Y 3 X Y 1 Then What Is X Y Quora

Www Cimt Org Uk Projects Mepres Step Up Mepanswers Pdf

Solving Systems Of Equations

Solve For X And Y 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2

Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf

Step By Step Math Wolfram Alpha Blog

Solve The Pair Of Equations 2 X 3 Y 13 5 X 4 Y 2 Youtube

Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y

Solve The System Of Eq 2x 3y 17 3x 2y 6 By Method Of Cross Multiplication Brainly In

What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora

5 X 3 Y 1 3 2x 2 3y 5 Brainly In